
এই পাঠ শেষে যা যা শিখতে পারবে-
১। অ্যাডার সার্কিট ব্যাখ্যা করতে পারবে।
২। হাফ অ্যাডার সার্কিট বিস্তারিত ব্যাখ্যা করতে পারবে।
৩। ফুল অ্যাডার সার্কিট বিস্তারিত ব্যাখ্যা করতে পারবে।
৪। হাফ অ্যাডার সার্কিট এর সাহায্যে ফুল অ্যাডার সার্কিট বাস্তবায়ন করতে পারবে।
৫। বাইনারি অ্যাডার সার্কিট ব্যাখ্যা করতে পারবে।
Go for English Version
অ্যাডার (Adder Circuit) কী বা যোগের বর্তনী কী?
যে সমবায় সার্কিট দ্বারা যোগের কাজ সম্পন্ন হয় তাকে অ্যাডার বা যোগের বর্তনী বলে।
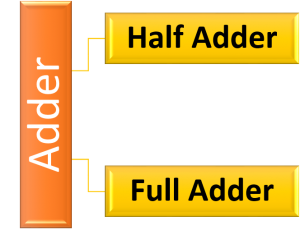
কম্পিউটারের সকল গাণিতিক কাজ বাইনারি যোগের মাধ্যমে সম্পন্ন হয়। গুণ হলো বার বার যোগ করা এবং ভাগ হলো বার বার বিয়োগ করা। আবার পূরক পদ্ধতিতে বাইনারি যোগের মাধ্যমেই বিয়োগ করা যায়। কাজেই যোগ করতে পারা মানেই হলো গুণ, বিয়োগ এবং ভাগ করতে পারা। অ্যাডার সার্কিট দুই ধরনের। যথা:
- হাফ অ্যাডার সার্কিট (Half Adder Circuit) বা অর্ধ যোগের বর্তনী
- ফুল অ্যাডার সার্কিট (Full Adder Circuit) বা পূর্ণ যোগের বর্তনী
হাফ অ্যাডার কী? (অর্ধ যোগের বর্তনী)
যে সমবায় সার্কিট দুটি বিট যোগ করে একটি যোগফল(S) ও একটি ক্যারি(C) আউটপুট দেয় তাকে হাফ অ্যাডার সার্কিট বা অর্ধযোগের বর্তনী বলে।
 চিত্রঃ হাফ অ্যাডারের ব্লক চিত্র
চিত্রঃ হাফ অ্যাডারের ব্লক চিত্র
হাফ অ্যাডার দুটি বিট যোগ করতে পারে। সুতরাং দুটি বিট দিয়ে চার ধরনের ভিন্ন ভিন্ন ইনপুট সেট তৈরি করা যায়। নিম্নে ভিন্ন ভিন্ন চার ধরনের ইনপুট সেট এর জন্য আউটপুট সত্যক সারণিতে দেখানো হলো-
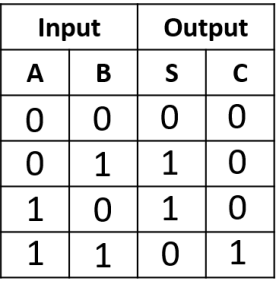
চিত্রঃ হাফ অ্যাডারের সত্যক সারণি
হাফ অ্যাডারের সত্যক সারণি থেকে দেখতে পাই আউটপুট sum হলো Exclusive-OR গেইট এর আউটপুট এবং আউটপুট carry হলো AND গেইট এর আউটপুট। সুতরাং হাফ অ্যাডারের বুলিয়ান এক্সপ্রেশন হলো-
sum এর ক্ষেত্রে-
S = A XOR B = A ⊕ B
carry এর ক্ষেত্রে-
C= A AND B = A.B
sum এবং carry এর বুলিয়ান এক্সপ্রেশন ব্যবহার করে হাফ অ্যাডারের সার্কিট
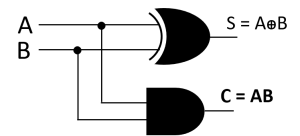
চিত্রঃ হাফ অ্যাডারের সার্কিট
♦ ভিডিও লেকচার পেতে YouTube চ্যানেলটিতে Subscribe করো।
♦ HSC ICT তৃতীয় অধ্যায়ের নোট পেতে ক্লিক করো।
♦ ICT সম্পর্কিত যেকোন প্রশ্নের উত্তর জানতে Facebook গ্রুপে যুক্ত হও।
শুধুমাত্র মৌলিক গেইট ব্যবহার করে হাফ অ্যাডার এর লজিক সার্কিটঃ
হাফ অ্যাডারের সত্যক সারণি থেকে SOP নিয়মানুসারে sum এবং carry এর নিম্নরূপ বুলিয়ান এক্সপ্রেশন পাওয়া যায়-
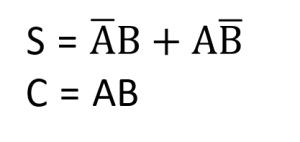
sum এবং carry এর বুলিয়ান এক্সপ্রেশন ব্যবহার করে হাফ অ্যাডারের সার্কিট
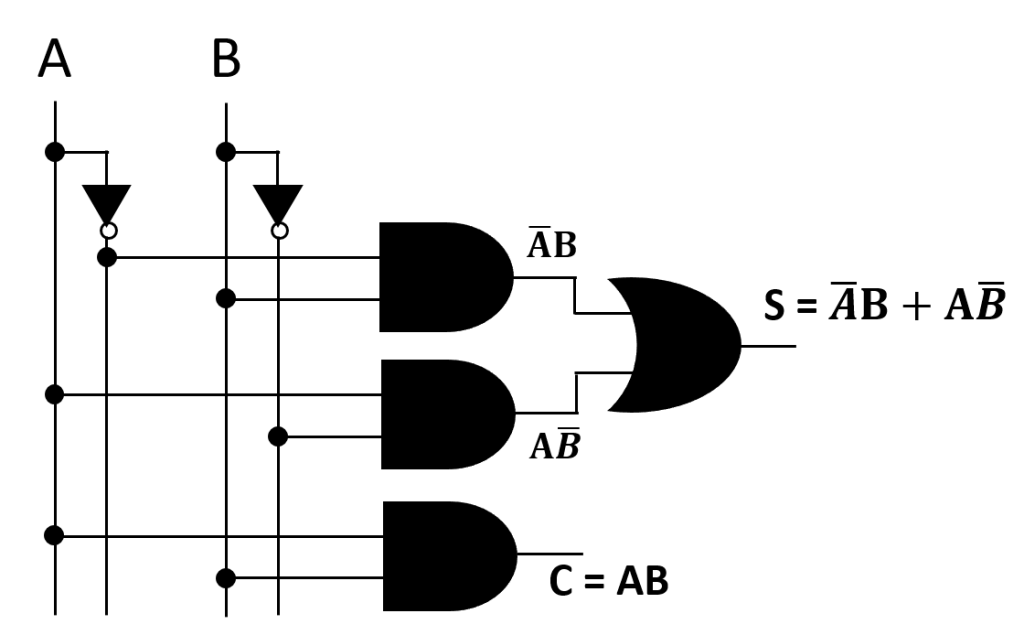
চিত্রঃ হাফ অ্যাডারের সার্কিট (শুধুমাত্র মৌলিক গেইটের সাহায্যে)
- শুধুমাত্র NAND গেইটের সাহায্যে হাফ-অ্যাডারের সার্কিট তৈরি বা বাস্তবায়ন কর।
- শুধুমাত্র NOR গেইটের সাহায্যে হাফ-অ্যাডারের সার্কিট তৈরি বা বাস্তবায়ন কর।
হাফ অ্যাডারের অসুবিধা:
হাফ অ্যাডার সার্কিটের একটি বড় অসুবিধা হলো যখন এটি বাইনারি অ্যাডার হিসাবে ব্যবহৃত হয়, কারণ একাধিক ডেটা বিট যোগ করার সময় পূর্ববর্তী সার্কিট থেকে “ক্যারি-ইন” করার বিধান নেই।
উদাহরণস্বরূপ, আমরা দুটি ৮-বিটের ডেটা একসাথে যুক্ত করতে চাই , এক্ষেত্রে ফলাফলে যে কোন ক্যারি বিটকে পরবর্তী ধাপে “রিপল” বা যুক্ত করতে সক্ষম হতে হবে।
হাফ অ্যাডার সবচেয়ে জটিল ক্রিয়াকলাপটি করতে পারে “1 + 1”, কিন্তু হাফ অ্যাডারে কোনও ক্যারি ইনপুট না
থাকায় ফলাফলটি ভুল হবে। এই সমস্যাটি কাটিয়ে ওঠার একটি সহজ উপায় হল বাইনারি অ্যাডার হিসাবে ফুল অ্যাডার সার্কিট ব্যবহার করা।
HSC ICT তৃতীয় অধ্যায়ের গুরুত্বপূর্ণ টপিকসমূহ
সংখ্যা পদ্ধতি এর টপিকসমূহঃ
- সংখ্যা পদ্ধতির ধারণা
- ডেসিমেল সংখ্যাকে বাইনারি, অক্টাল এবং হেক্সাডেসিমেল সংখ্যায় রূপান্তর
- বাইনারি, অক্টাল ও হেক্সাডেসিমেল সংখ্যাকে ডেসিমেল সংখ্যায় রূপান্তর
- বাইনারি, অক্টাল ও হেক্সাডেসিমেল সংখ্যাসমূহের পারস্পরিক রূপান্তর
- চিহ্নযুক্ত সংখ্যা এবং এর উপস্থাপন
- কোড ( BCD, EBCDIC, ASCII, ইউনিকোড )
ডিজিটাল ডিভাইস এর টপিকসমূহঃ
- মৌলিক লজিক গেট (AND, OR, NOT )
- সার্বজনীন গেইট(NOR, NAND) ও বিশেষ গেইট(XOR, XNOR)
- NAND ও NOR গেটের সার্বজনীনতা প্রমাণ
- এনকোডার এবং ডিকোডার
- অ্যাডার সার্কিট (হাফ অ্যাডার ও ফুল অ্যাডার)
ফুল অ্যাডার কী? (পূর্ণ যোগের বর্তনী)
যে সমবায় সার্কিট তিনটি বাইনারি বিট (দুটি ইনপুট বিট ও একটি ক্যারি বিট) যোগ করে একটি যোগফল(S) এবং বর্তমান ক্যারি(C0) আউটপুট দেয় তাকে ফুল অ্যাডার সার্কিট বা পূর্ণ যোগের বর্তনী বলে। ক্যারিসহ অপর দুটি বিট যোগ করার জন্য ফুল অ্যাডার সার্কিট ব্যবহৃত হয়। আবার দুটি হাফ অ্যাডার সার্কিট দ্বারা একটি ফুল অ্যাডারের কাজ করা যায়।

চিত্রঃ ফুল অ্যাডারের ব্লক চিত্র
ফুল অ্যাডার তিনটি বিট যোগ করতে পারে। সুতরাং তিনটি বিট দিয়ে আট ধরণের ভিন্ন ভিন্ন ইনপুট সেট তৈরি করা যায়। নিম্নে ভিন্ন ভিন্ন আট ধরনের ইনপুট সেট এর জন্য আউটপুট সত্যক সারণিতে দেখানো হলো-
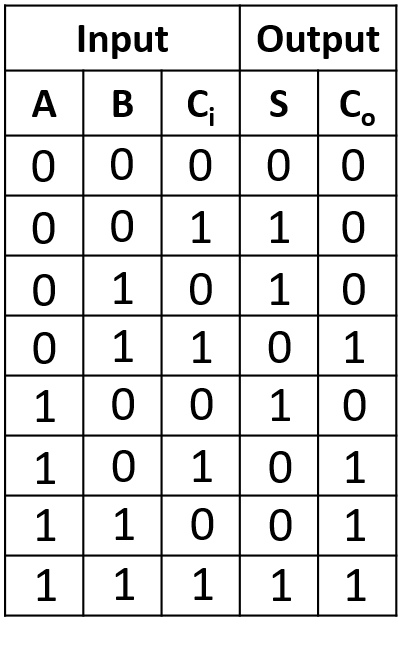
চিত্রঃ ফুল অ্যাডারের সত্যক সারণি
ফুল অ্যাডারের সত্যক সারণি থেকে SOP নিয়মানুসারে sum এবং carry এর নিম্নরূপ বুলিয়ান এক্সপ্রেশন পাওয়া যায়-
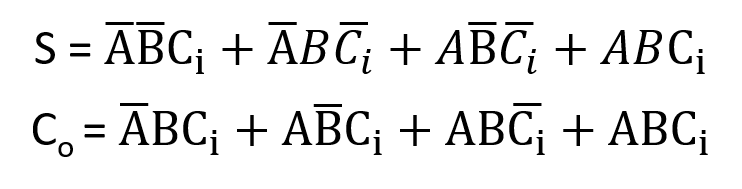
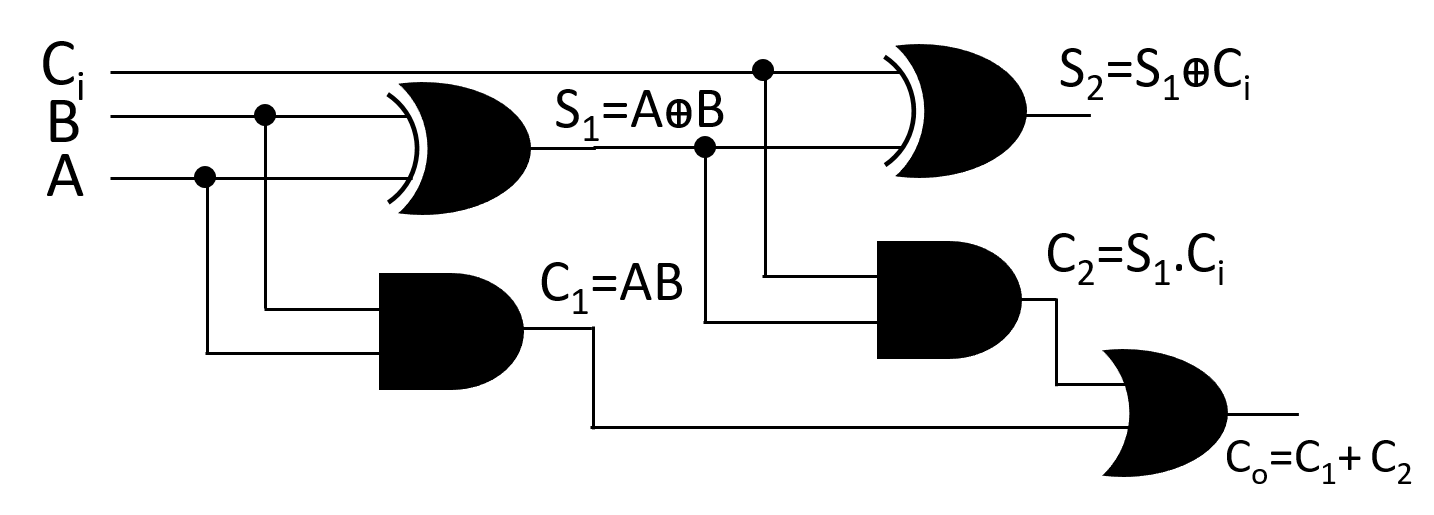
ফুল অ্যাডারের sum এবং carry এর বুলিয়ান এক্সপ্রেশন ব্যবহার করে সার্কিট
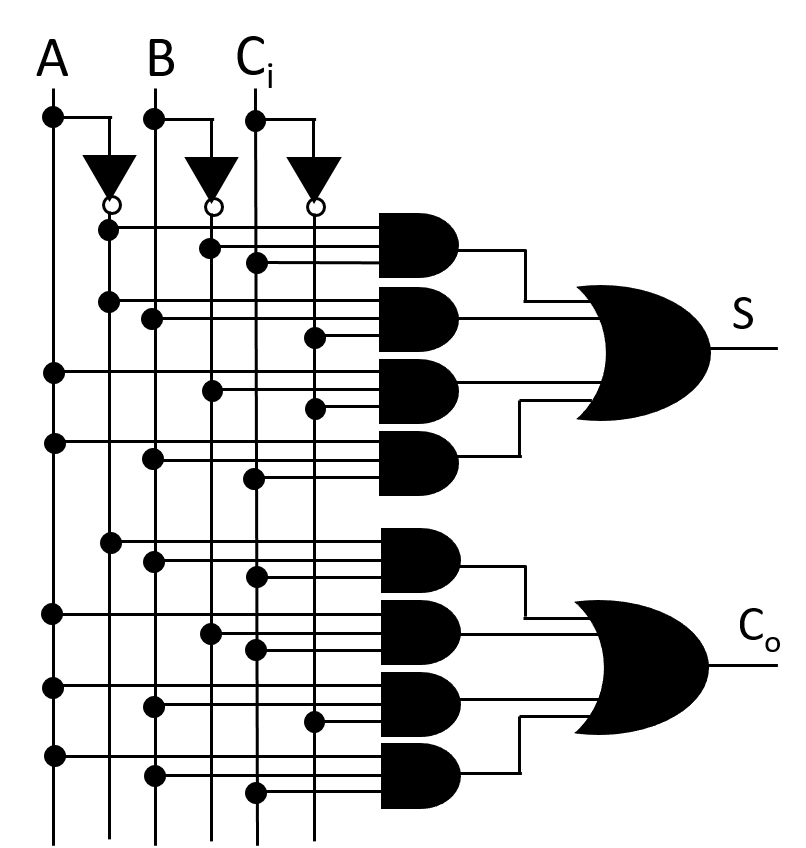
চিত্রঃ ফুল অ্যাডারের সার্কিট ( শুধুমাত্র মৌলিক গেইটের সাহায্যে )
ফুল অ্যাডারের বুলিয়ান এক্সপ্রেশন দুটি সরলীকরণ করে পাই-

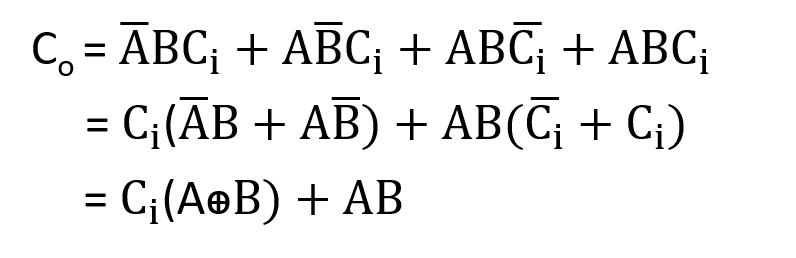
ফুল অ্যাডারের sum এবং carry এর সরলীকৃত এক্সপ্রেশনদুটি ব্যবহার করে সার্কিট
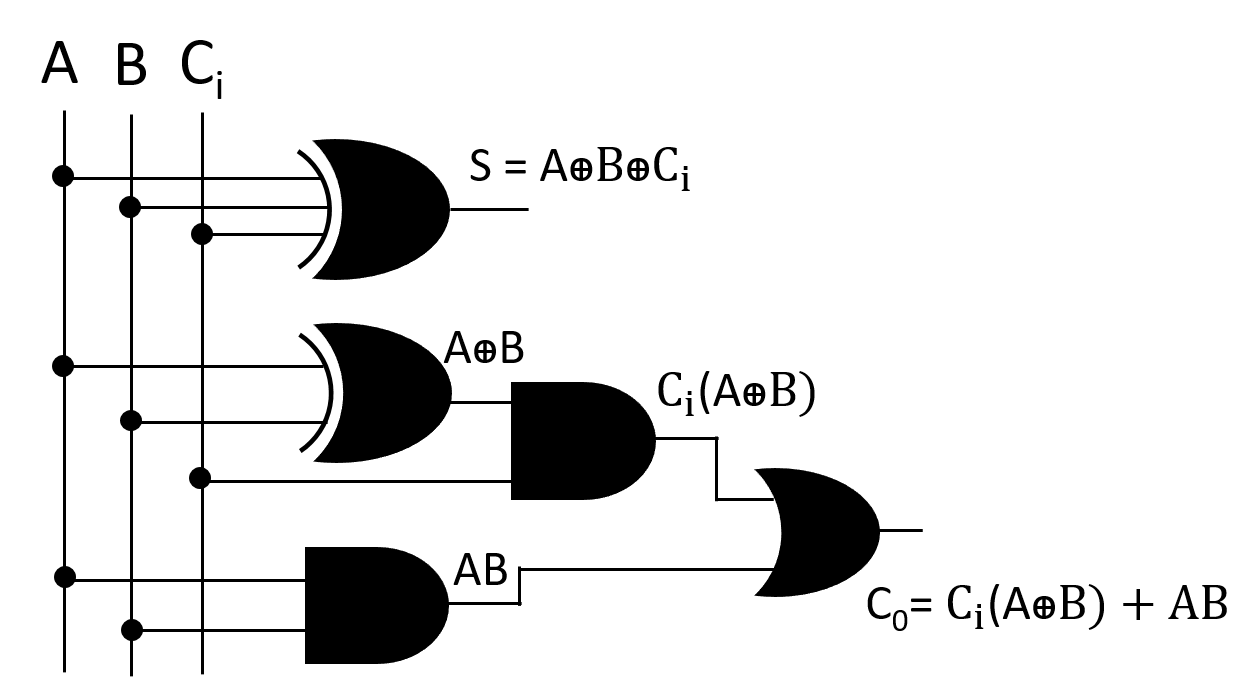
চিত্রঃ ফুল অ্যাডারের সার্কিট ( সরলীকৃত সমীকরণের )
- শুধুমাত্র NAND গেইটের সাহায্যে ফুল অ্যাডারের সার্কিট তৈরি বা বাস্তবায়ন কর।
- শুধুমাত্র NOR গেইটের সাহায্যে ফুল অ্যাডারের সার্কিট তৈরি বা বাস্তবায়ন কর।
হাফ অ্যাডারের সাহায্যে ফুল অ্যাডার বাস্তবায়ন
আমরা জানি, ফুল অ্যাডারের ইনপুট A, B ও Ci এবং আউটপুট যোগফল S ও ক্যারি Co হলে ফুল অ্যাডারের ক্ষেত্রে,
S = AꚚBꚚCi
Co=(AꚚB).Ci + A.B
উপরের ফাংশনদুটি বাস্তবায়নের লক্ষে দুটি হাফ অ্যাডার ও একটি অর গেইটের সাহায্যে নিমোক্ত সার্কিট তৈরি করা হলো-
চিত্রঃ হাফ অ্যাডারের সাহায্যে ফুল অ্যাডারের সার্কিট বাস্তবায়ন
প্রথম হাফ অ্যাডারের ক্ষেত্রে-
S1=AꚚB এবং
C1=A.B
দ্বিতীয় হাফ অ্যাডারের ক্ষেত্রে-
S2=S1ꚚCi এবং
C2=S1.Ci
S2=S1ꚚCi এই সমীকরণে S1=AꚚB বসিয়ে পাই S2= AꚚBꚚCi যা ফুল-অ্যাডারের যোগফল S ।
আবার Co=C1+C2 সমীকরণে C1 ও C2 এর মান বসিয়ে পাই Co=(AꚚB).Ci + A.B যা ফুল-অ্যাডারের আউটপুট ক্যারি Co । সুতরাং দুটি হাফ অ্যাডার ও একটি অর গেইটের সাহায্যে একটি ফুল অ্যাডার বাস্তবায়ন সম্ভব।
বাইনারি অ্যাডার কী?
যে অ্যাডার দুটি বাইনারি সংখ্যা যোগ করতে পারে তাকে বাইনারি অ্যাডার বলে। বাইনারি অ্যাডার দুই প্রকার। যথা-
- প্যারালাল বাইনারি অ্যাডার
- সিরিয়াল বাইনারি অ্যাডার
প্যারালাল বাইনারি অ্যাডার কী?
প্যারালাল বাইনারি অ্যাডার n বিটের দুইটি বাইনারি সংখ্যার বিটগুলোকে সমান্তরালে যোগ করতে পারে। শুধুমাত্র ফুল-অ্যাডার অথবা হাফ-অ্যাডার এবং ফুল-অ্যাডারের সাহায্যে প্যারালাল বাইনারি অ্যাডার সার্কিট তৈরি করা যায়। প্যারালাল বাইনারি অ্যাডার দিয়ে n বিটের দুইটি বাইনারি সংখ্যা যোগ করার জন্য একটি হাফ-অ্যাডার ও (n-1) সংখ্যক ফুল-অ্যাডার ব্যবহৃত হয়। তবে n বিটের দুইটি বাইনারি সংখ্যার যোগ শুধুমাত্র n সংখ্যক ফুল-অ্যাডার ব্যবহার করেও করা যায়। এক্ষেত্রে প্রথম ফুল অ্যাডারের ইনপুট ক্যারিটি গ্রাউন্ডেড (ক্যারি জিরো) করে রাখা হয়।
প্যারালাল বাইনারি অ্যাডার বা বাইনারি অ্যাডারের সাহায্যে দুইটি বাইনারি সংখ্যা A4A3A2A1 এবং B4B3B2B1 এর যোগঃ
হাফ-অ্যাডার এবং ফুল-অ্যাডার ব্যবহার করে:
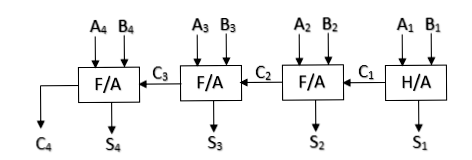
চিত্রঃ ৪-বিট বাইনারি প্যারালাল অ্যাডার
শুধুমাত্র ফুল অ্যাডার ব্যবহার করে:
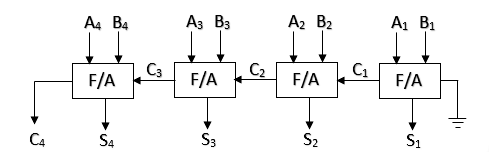
চিত্রঃ ৪-বিট বাইনারি প্যারালাল অ্যাডার
উদাহরণ-১: বাইনারি অ্যাডার সার্কিটের সাহায্যে 1101 এবং 1110 যোগ।
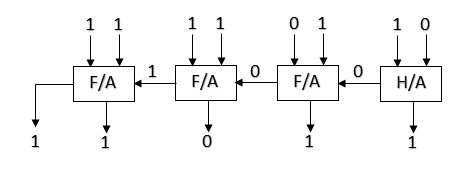
সুতরাং (1101)2 + (1110)2 = (11011)2
উদাহরণ-2: বাইনারি অ্যাডার সার্কিটের সাহায্যে 11011 এবং 10101 যোগ কর।
উদাহরণ-3: বাইনারি অ্যাডার সার্কিটের সাহায্যে 110 এবং 111 যোগ কর।
সিরিয়াল বাইনারি অ্যাডার কী?
সিরিয়াল বাইনারি অ্যাডার n বিটের দুইটি বাইনারি সংখ্যার বিটগুলোকে বিট-বাই-বিট যোগ করে থাকে। একটি ফ্লিপ-ফ্লপ এবং একটি ফুল-অ্যাডার দিয়ে সিরিয়াল বাইনারি অ্যাডার সার্কিট তৈরি করা যায়। প্রতিটি ক্লক পালসে ফুল অ্যাডার সার্কিট দুইটি বাইনারি সংখ্যার একটি করে বিট যোগ করে sum এবং আউটপুট carry দেয়। পরবর্তী ক্লক পালসে পূর্ববর্তী আউটপুট ক্যারি এবং পরবর্তী দুইটি বিট যোগ করে sum এবং আউটপুট carry দেয়। এইভাবে n বিটের দুইটি বাইনারি সংখ্যার বিটগুলোকে বিট-বাই-বিট যোগ করে থাকে।
HSC ICT এর সকল অধ্যায়
- প্রথম অধ্যায়ের টপিকসমূহ
- দ্বিতীয় অধ্যায়ের টপিকসমূহ
- তৃতীয় অধ্যায়ের টপিকসমূহ
- চতুর্থ অধ্যায়ের টপিকসমূহ
- পঞ্চম অধ্যায়ের টপিকসমূহ
- ষষ্ঠ অধ্যায়ের টপিকসমূহ
পাঠ মূল্যায়ন-
জ্ঞানমূলক প্রশ্নসমূহঃ
ক। অ্যাডার কী?
ক। হাফ অ্যাডার কী?
ক। ফুল অ্যাডার কী?
খ। বাইনারি অ্যাডার কী?
অনুধাবনমূলক প্রশ্নসমূহঃ
খ। “কম্পিউটার একটি পদ্ধতিতেই সকল গাণিতিক কাজ করে থাকে”-ব্যাখ্যা কর।
সৃজনশীল প্রশ্নসমূহঃ
ব্লক চিত্রগুলো লক্ষ কর এবং নিচের প্রশ্নের উত্তর দাও:

ব্লক চিত্র-১ ব্লক চিত্র-২
গ) ব্লক চিত্র-১ এর যুক্তি বর্তনী শুধুমাত্র NAND গেইট দ্বারা বাস্তবায়ন কর।
ঘ) ব্লক চিত্র-১ দ্বারা ব্লক চিত্র-২ এর সার্কিট বাস্তবায়ন করা যায় কি না- বিশ্লেষণ করে মতামত দাও।
ব্লক চিত্রগুলো লক্ষ কর এবং নিচের প্রশ্নের উত্তর দাও:
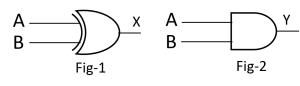
গ) Fig-1 ও Fig-2 এর সমন্বয়ে তৈরি যোগের বর্তনীটি বর্ণনা কর।
ঘ) বাইনারি যোগের বর্তনী তৈরিতে চিত্রদ্বয়ের ভূমিকা বিশ্লেষণ কর।
চিত্রটি লক্ষ কর এবং নিচের প্রশ্নের উত্তর দাও:
গ) উদ্দীপক চিত্রটির বর্তনী মৌলিক গেইট দিয়ে বাস্তবায়ন কর।
ঘ) উদ্দীপকের বর্তনীটিতে একটি ইনপুট হ্রাস করলে নতুন যে বর্তনীটি পাওয়া যাবে তা NOR গেইট দ্বারা বাস্তবায়ন কর।
চিত্রগুলো লক্ষ কর এবং নিচের প্রশ্নের উত্তর দাও:

গ) চিত্র-১ ও চিত্র-২ এর সমন্বয়ে তৈরি যোগের বর্তনীটি বর্ণনা কর।
ঘ) চিত্র-১ ও চিত্র-২ এর সমন্বিত বর্তনী দ্বারা চিত্র-৩ বাস্তবায়ন সম্ভব- বিশ্লেষণপূর্বক মতামত দাও।
বহুনির্বাচনি প্রশ্নসমূহঃ
১। নিচের কোনটি যোগের ক্ষেত্রে ব্যবহৃত হয়?
ক) এনকোডার খ) ডিকোডার গ) অ্যাডার ঘ) কাউন্টার
২। একটি ৪ বিট বাইনারি অ্যাডার তৈরি করতে ব্যবহৃত হয়-
i. চারটি ফুল অ্যাডার
ii. তিনটি ফুল অ্যাডার ও একটি হাফ অ্যাডার
iii. তিনটি হাফ অ্যাডার ও একটি ফুল অ্যাডার
নিচের কোনটি সঠিক?
ক) i ও ii খ) i ও iii গ) ii ও iii ঘ) i, ii ও iii
৩। হাফ অ্যাডারে ইনপুট সংখ্যা কত?
ক) ১ খ) ২ গ) ৩ ঘ) ৪
৪। ফুল অ্যাডারে ইনপুট সংখ্যা কত?
ক) ১ খ) ২ গ) ৩ ঘ) ৪
৫। হাফ অ্যাডারের বুলিয়ান এক্সপ্রেশন হল-
i. C=A+B ii. C=AB iii. S=A⊕B
নিচের কোনটি সঠিক?
ক) i ও ii খ) i ও iii গ) ii ও iii ঘ) i, ii ও iii
৬। ফুল অ্যাডারের তিনটি বিটের সর্বোচ্চ যোগফল হবে-
i. (3)10 ii. (11)2 iii. (111)2
নিচের কোনটি সঠিক?
ক) i ও ii খ) i ও iii গ) ii ও iii ঘ) i, ii ও iii
তৃতীয় অধ্যায়ের সকল MCQ দেখতে ক্লিক করো
Written by,
- Mizanur Rahman (Mizan)
- Lecturer in ICT, Shaheed Bir Uttam Lt. Anwar Girls’ College , Dhaka Cantonment
- Founder & Author at www.edupointbd.com
- Software Engineer at mands IT
- Former Lecturer in ICT, Cambrian College, Dhaka
- Contact: 01724351470

wow sir
Sir,would you please give me the answer of the sample questions?
Tnx
Thanks sir
C programme er need video download algorithms and flowchart.