এই পাঠ শেষে যা যা শিখতে পারবে-
১। অক্টাল এবং হেক্সাডেসিমেল সংখ্যাকে বাইনারি সংখ্যায় রূপান্তর করতে পারবে।
২। বাইনারি সংখ্যাকে অক্টাল এবং হেক্সাডেসিমেল সংখ্যায় রূপান্তর করতে পারবে।
৩। অক্টাল সংখ্যাকে হেক্সাডেসিমেল সংখ্যায় রূপান্তর করতে পারবে।
৪। হেক্সাডেসিমেল সংখ্যাকে অক্টাল সংখ্যায় রূপান্তর করতে পারবে।
Go for English Version
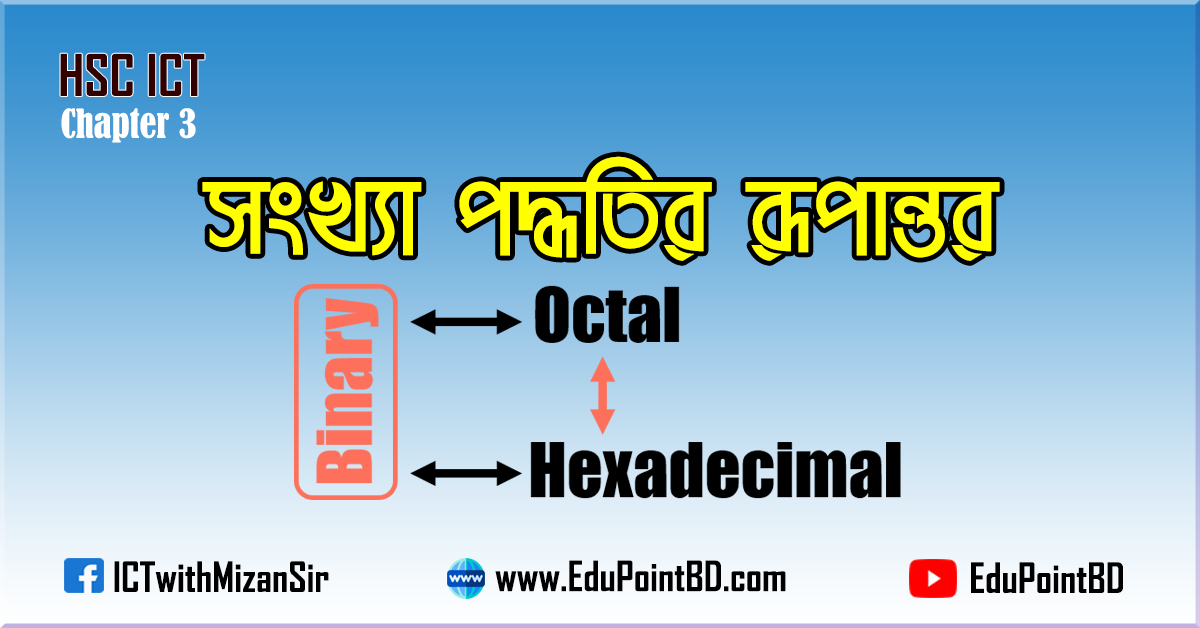
নন-ডেসিমেল অর্থাৎ বাইনারি, অক্টাল ও হেক্সাডেসিমেল সংখ্যাগুলোর মধ্যে নিম্নরুপে পারস্পারিক রূপান্তর করা যায়-
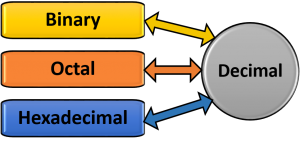
ধাপ-১ঃ প্রদত্ত যেকোন সংখ্যা পদ্ধতির সংখ্যাকে প্রথমে ডেসিমেলে রূপান্তর
ধাপ-২ঃ প্রাপ্ত ডেসিমেল সংখ্যাকে টার্গেট সংখ্যা পদ্ধতিতে রূপান্তর
অর্থাৎ নন-ডেসিমেল সংখ্যাগুলোর মধ্যে পারস্পারিক রূপান্তরের ক্ষেত্রে দুটি ধাপে সকল রূপান্তর করা যায়।
এছাড়া 2n (যেখানে, n=0,1,2,3,…..) ফর্মুলা ব্যবহার করেও সরাসরি অক্টাল ও হেক্সাডেসিমেল থেকে বাইনারি এবং বাইনারি থেকে অক্টাল ও হেক্সাডেসিমেলে রূপান্তর করা যায়।
- অক্টালের ক্ষেত্রে 4 2 1 ( 2n ; যেখানে, n=0,1,2)
- হেক্সাডেসিমেলের ক্ষেত্রে 8 4 2 1 ( 2n ; যেখানে, n=0,1,2,3)
নিয়ম অনুসরণ করে নিচে আলোচনা করা হলো-
♦ ভিডিও লেকচার পেতে YouTube চ্যানেলটিতে Subscribe করো।
♦ HSC ICT তৃতীয় অধ্যায়ের নোট পেতে ক্লিক করো।
♦ ICT সম্পর্কিত যেকোন প্রশ্নের উত্তর জানতে Facebook গ্রুপে যুক্ত হও।
অক্টাল সংখ্যাকে বাইনারি সংখ্যায় রূপান্তর:
পূর্ণ সংখ্যা এবং ভগ্নাংশের ক্ষেত্রে একই নিয়ম–
ধাপ-১ঃ অক্ট্যাল সংখ্যার প্রতিটি ডিজিটের তিন বিট বাইনারি মান লিখতে হবে। [ 4 2 1 ফর্মুলা ব্যবহার করে ]
[প্রতিটি ডিজিটের বাইনারি মান ৩-বিটের কম হলে বাম পার্শ্বে প্রয়োজনীয় সংখ্যক শুন্য বসিয়ে ৩-বিট পূর্ণ করতে হবে। প্রতিটি ডিজিটের তিন বিট লেখার কারণ, অক্টাল সংখ্যার প্রতিটি ডিজিটকে ম্যাক্সিমাম তিন বিটের মাধ্যমেই প্রকাশ করা যায় ]
ধাপ-২ঃ অবশেষে প্রাপ্ত বাইনারি মান গুলিকে পাশাপাশি সাজিয়ে লিখলে অক্ট্যাল সংখ্যাটির সমতূল্য বাইনারি সংখ্যা পাওয়া যাবে।
উদাহরণঃ (375.24)8 সংখ্যাকে বাইনারি সংখ্যায় রূপান্তর।
সুতরাং (375.24)8 = (011111101.010110)2
- (127)8 কে বাইনারি সংখ্যা পদ্ধতিতে রূপান্তর কর।
- (.7125)8 কে বাইনারি সংখ্যা পদ্ধতিতে রূপান্তর কর।
হেক্সাডেসিমেল সংখ্যাকে বাইনারি সংখ্যায় রূপান্তরঃ
পূর্ণ সংখ্যা এবং ভগ্নাংশের ক্ষেত্রে একই নিয়ম–
ধাপ-১ঃ হেক্সাডেসিমেল সংখ্যার প্রতিটি ডিজিটের চার বিট বাইনারি মান লিখতে হবে। [ 8 4 2 1 ফর্মুলা ব্যবহার করে ]
[প্রতিটি ডিজিটের বাইনারি মান ৪-বিটের কম হলে বাম পার্শ্বে প্রয়োজনীয় সংখ্যক শুন্য বসিয়ে ৪-বিট পূর্ণ করতে হবে। প্রতিটি ডিজিটের চার বিট লেখার কারণ, হেক্সাডেসিমেল সংখ্যার প্রতিটি ডিজিটকে ম্যাক্সিমাম চার বিটের মাধ্যমেই প্রকাশ করা যায় ]
ধাপ-২ঃ অবশেষে প্রাপ্ত বাইনারি মান গুলিকে পাশাপাশি সাজিয়ে লিখলে হেক্সাডেসিমেল সংখ্যাটির সমতূল্য বাইনারি সংখ্যা পাওয়া যাবে।
উদাহরণঃ (35D.4F)16 সংখ্যাকে বাইনারি সংখ্যায় রূপান্তর।
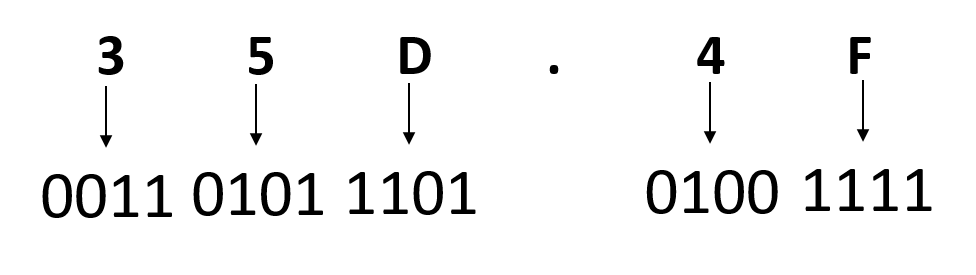
সুতরাং (35D.4F)16 = (001101011101.01001111)2
- (D218)16 কে বাইনারি সংখ্যা পদ্ধতিতে রূপান্তর কর।
- (.1C39)16 কে বাইনারি সংখ্যা পদ্ধতিতে রূপান্তর কর।
বাইনারি সংখ্যাকে অক্টাল সংখ্যায় রূপান্তরঃ
ধাপ-১ঃ পূর্ণ সংখ্যার ক্ষেত্রে সংখ্যাটির ডান থেকে বাম দিকে ৩-বিট করে গ্রুপ করে নিতে হবে এবং ভগ্নাংশের ক্ষেত্রে বাম থেকে ডান দিকে ৩-বিট করে গ্রুপ করতে হবে ।
[৩-বিটের কম হলে পূর্ণ সংখ্যার ক্ষেত্রে বাম পার্শ্বে প্রয়োজনীয় সংখ্যক শুন্য বসিয়ে ৩-বিট পূর্ণ করতে হবে এবং ভগ্নাংশের ক্ষেত্রে ডান পার্শ্বে প্রয়োজনীয় সংখ্যক শুন্য বসিয়ে ৩-বিট পূর্ণ করতে হবে ]
[পূর্নাংশের ক্ষেত্রে বাম দিকে গ্রুপ করার কারণ সর্ব বামে অতিরিক্ত শূন্য বসালে মানের কোন পরিবর্তন হয় না অনুরূপ ভাবে ভগ্নাংশের ক্ষেত্রে ডান দিকে গ্রুপ করার কারণ সর্ব ডানে অতিরিক্ত শূন্য বসালে মানের কোন পরিবর্তন হয় না ]
ধাপ-২ঃ অতপর প্রতিটি ৩-বিট গ্রুপের আলাদা ভাবে অক্টাল মান লিখতে হবে।
[ প্রতিটি বাইনারি গ্রুপে যে কয়টি ১ আছে তাদের স্থানীয় মানসমূহ যোগ করলে ঐ বাইনারি গ্রুপের সমমান অক্টাল মান পাওয়া যাবে ]
ধাপ-৩ঃ অবশেষে প্রাপ্ত অক্টাল মান গুলিকে পাশাপাশি সাজিয়ে লিখলে বাইনারি সংখ্যাটির সমতূল্য অক্টাল সংখ্যা পাওয়া যাবে।
উদাহরণঃ (10101011.1011011)2 সংখ্যাকে অক্টাল সংখ্যায় রূপান্তর।
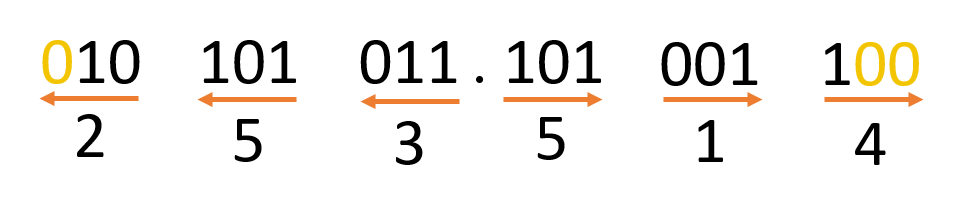
সুতরাং (10101011.1011011)2 =(253.514)8
- (1101001)2 কে অক্টাল সংখ্যা পদ্ধতিতে রূপান্তর কর।
- (.1010011)2 কে অক্টাল সংখ্যা পদ্ধতিতে রূপান্তর কর।
বাইনারি সংখ্যাকে হেক্সাডেসিমেল সংখ্যায় রূপান্তরঃ
ধাপ-১ঃ পূর্ণ সংখ্যার ক্ষেত্রে সংখ্যাটির ডান থেকে বাম দিকে ৪-বিট করে গ্রুপ করে নিতে হবে এবং ভগ্নাংশের ক্ষেত্রে বাম থেকে ডান দিকে ৪-বিট করে গ্রুপ করতে হবে ।
[৪-বিটের কম হলে পূর্ণ সংখ্যার ক্ষেত্রে বাম পার্শ্বে প্রয়োজনীয় সংখ্যক শুন্য বসিয়ে ৪-বিট পূর্ণ করতে হবে এবং ভগ্নাংশের ক্ষেত্রে ডান পার্শ্বে প্রয়োজনীয় সংখ্যক শুন্য বসিয়ে ৪-বিট পূর্ণ করতে হবে ]
[পূর্নাংশের ক্ষেত্রে বাম দিকে গ্রুপ করার কারণ সর্ব বামে অতিরিক্ত শূন্য বসালে মানের কোন পরিবর্তন হয় না অনুরূপ ভাবে ভগ্নাংশের ক্ষেত্রে ডান দিকে গ্রুপ করার কারণ সর্ব ডানে অতিরিক্ত শূন্য বসালে মানের কোন পরিবর্তন হয় না ]
ধাপ-২ঃ অতপর প্রতিটি ৪-বিট গ্রুপের আলাদা ভাবে হেক্সাডেসিমেল মান লিখতে হবে।
[ প্রতিটি বাইনারি গ্রুপে যে কয়টি ১ আছে তাদের স্থানীয় মানসমূহ যোগ করলে ঐ বাইনারি গ্রুপের সমমান হেক্সাডেসিমেল মান পাওয়া যাবে ]
ধাপ-৩ঃ অবশেষে প্রাপ্ত হেক্সাডেসিমেল মান গুলিকে পাশাপাশি সাজিয়ে লিখলে বাইনারি সংখ্যাটির সমতূল্য হেক্সাডেসিমেল সংখ্যা পাওয়া যাবে।
উদাহরণঃ (0111001011.1010011)2 সংখ্যাকে হেক্সাডেসিমেল সংখ্যায় রূপান্তর।
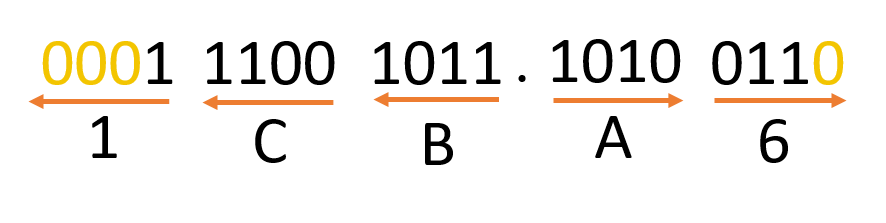
সুতরাং (0111001011.1010011)2 = (1CB.A6)16
- (1101101)2 কে হেক্সাডেসিমেল সংখ্যা পদ্ধতিতে রূপান্তর কর।
- (.1010011)2 কে হেক্সাডেসিমেল সংখ্যা পদ্ধতিতে রূপান্তর কর।
HSC ICT তৃতীয় অধ্যায়ের গুরুত্বপূর্ণ টপিকসমূহ
সংখ্যা পদ্ধতি এর টপিকসমূহঃ
- সংখ্যা পদ্ধতির ধারণা
- ডেসিমেল সংখ্যাকে বাইনারি, অক্টাল এবং হেক্সাডেসিমেল সংখ্যায় রূপান্তর
- বাইনারি, অক্টাল ও হেক্সাডেসিমেল সংখ্যাকে ডেসিমেল সংখ্যায় রূপান্তর
- বাইনারি, অক্টাল ও হেক্সাডেসিমেল সংখ্যাসমূহের পারস্পরিক রূপান্তর
- চিহ্নযুক্ত সংখ্যা এবং এর উপস্থাপন
- কোড ( BCD, EBCDIC, ASCII, ইউনিকোড )
ডিজিটাল ডিভাইস এর টপিকসমূহঃ
- মৌলিক লজিক গেট (AND, OR, NOT )
- সার্বজনীন গেইট(NOR, NAND) ও বিশেষ গেইট(XOR, XNOR)
- NAND ও NOR গেটের সার্বজনীনতা প্রমাণ
- এনকোডার এবং ডিকোডার
- অ্যাডার সার্কিট (হাফ অ্যাডার ও ফুল অ্যাডার)
অক্টাল সংখ্যাকে হেক্সাডেসিমেল সংখ্যায় রূপান্তরঃ
ধাপ-১ঃ প্রথমে অক্টাল সংখ্যাটিকে বাইনারি সংখ্যায় রুপান্তর করতে হবে
ধাপ-২ঃ প্রাপ্ত বাইনারি সংখ্যাটিকে হেক্সাডেসিমেল সংখ্যায় রূপান্তর করতে হবে
অথবা
ধাপ-১ঃ প্রথমে অক্টাল সংখ্যাটিকে ডেসিমেল সংখ্যায় রুপান্তর করতে হবে
ধাপ-২ঃ প্রাপ্ত ডেসিমেল সংখ্যাটিকে হেক্সাডেসিমেল সংখ্যায় রূপান্তর করতে হবে
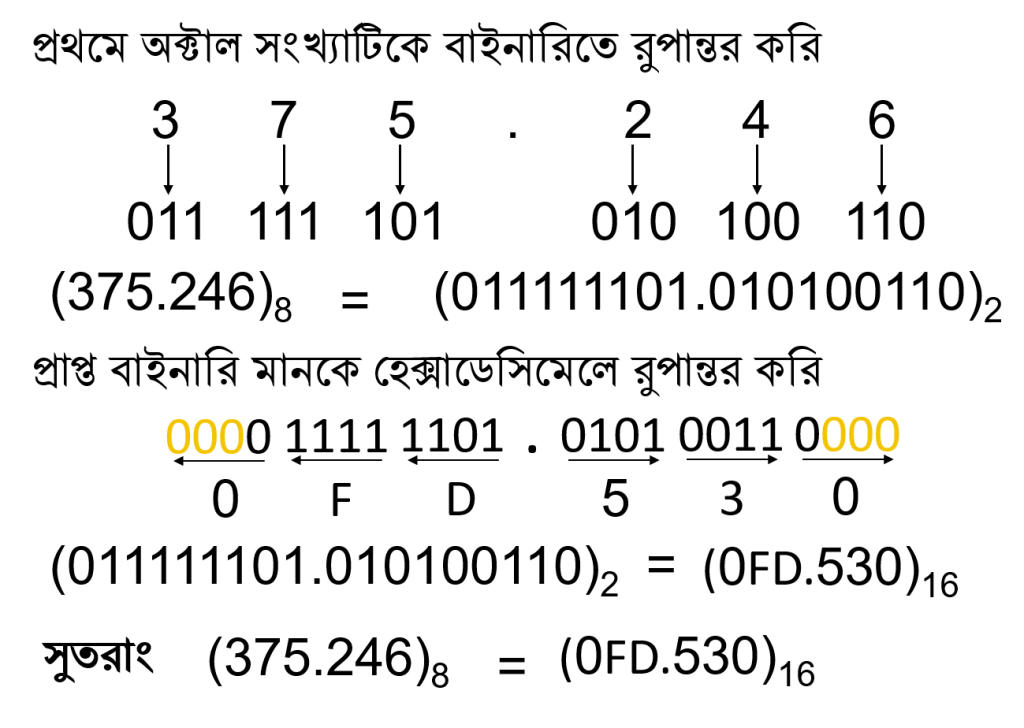
উদাহরণঃ (375.246)8 সংখ্যাকে হেক্সাডেসিমেল সংখ্যায় রূপান্তর।
- (5273)8 কে হেক্সাডেসিমেল সংখ্যা পদ্ধতিতে রূপান্তর কর।
- (.5137)8 কে হেক্সাডেসিমেল সংখ্যা পদ্ধতিতে রূপান্তর কর।
হেক্সাডেসিমেল সংখ্যাকে অক্টাল সংখ্যায় রূপান্তরঃ
ধাপ-১ঃ প্রথমে হেক্সাডেসিমেল সংখ্যাটিকে বাইনারি সংখ্যায় রুপান্তর করতে হবে
ধাপ-২ঃ প্রাপ্ত বাইনারি সংখ্যাটিকে অক্টাল সংখ্যায় রূপান্তর করতে হবে
অথবা
ধাপ-১ঃ প্রথমে হেক্সাডেসিমেল সংখ্যাটিকে ডেসিমেল সংখ্যায় রুপান্তর করতে হবে
ধাপ-২ঃ প্রাপ্ত ডেসিমেল সংখ্যাটিকে অক্টাল সংখ্যায় রূপান্তর করতে হবে
উদাহরণঃ (08B.FCD)16 সংখ্যাকে অক্টাল সংখ্যায় রূপান্তর।

- (5F293)16 কে অক্টাল সংখ্যা পদ্ধতিতে রূপান্তর কর।
- (.A127)16 কে অক্টাল সংখ্যা পদ্ধতিতে রূপান্তর কর।
HSC ICT এর সকল অধ্যায়
- প্রথম অধ্যায়ের টপিকসমূহ
- দ্বিতীয় অধ্যায়ের টপিকসমূহ
- তৃতীয় অধ্যায়ের টপিকসমূহ
- চতুর্থ অধ্যায়ের টপিকসমূহ
- পঞ্চম অধ্যায়ের টপিকসমূহ
- ষষ্ঠ অধ্যায়ের টপিকসমূহ
পাঠ মূল্যায়ন-
উদ্দীপকটি পড় এবং প্রশ্নের উত্তর দাওঃ
ICT বিষয়ের অধ্যাপক ক্লাশে সংখ্যা পদ্ধতি পড়াচ্ছিলেন। তখন ইমরানকে তার ICT বিষয়ের অর্ধ-বার্ষিক ও বার্ষিক পরীক্ষার প্রাপ্ত নম্বর জানতে চাইলে সে বলল, অর্ধ-বার্ষিকে (37)8 এবং বার্ষিক পরীক্ষায় (3F)16 নম্বর পেয়েছে। অন্যান্য ছাত্ররা এর অর্থ বুঝতে না পেরে স্যারকে জিজ্ঞেস করলে স্যার বিস্তারিত বুঝিয়ে বললেন।
গ) ইমরানের অর্ধ-বার্ষিক এবং বার্ষিক পরীক্ষায় প্রাপ্ত নম্বর কে বাইনারি সংখ্যায় রুপান্তর কর।
ঘ) উদ্দীপকে বর্ণিত ইমরানের অর্ধ-বার্ষিকের নম্বরকে হেক্সাডেসিমেল এবং বার্ষিক পরীক্ষায় প্রাপ্ত নম্বরকে অক্টাল সংখ্যায় রূপান্তর কর।
উদ্দীপকটি পড় এবং প্রশ্নের উত্তর দাওঃ
নাবিলা বাজারে গিয়ে (754.25)8 টাকার বই, (E54.2C1)16 টাকার কাগজ, (100)2 টাকার কলম কিনল। নাবিলার বন্ধু শর্মি (100101.010)2 টাকা খাবার ও (10110.110)2 টাকা যাতায়াত বাবদ ব্যয় করল।
গ) নাবিলার কাগজ ও কলম বাবদ মোট কতো টাকা খরচ হয়েছে তা বাইনারিতে প্রকাশ কর।
বহুনির্বাচনি প্রশ্নসমূহঃ
১। (১২৭)৮ এর সমকক্ষ বাইনারি সংখ্যা কোনটি?
ক) (১০১০১০১)২ খ) (১০১০১১১)২ গ) (১১১০১০১)২ ঘ) (১০১১১০১)২
২। 4C এর সমকক্ষ বাইনারি সংখ্যা কোনটি?
ক) 11001100 খ) 01001100 গ) 01001010 ঘ) 01001101
৩। রুবীনার বয়স (3A)16 বাইনারি সংখ্যায় তা কত হবে?
ক) 00111010 খ) 1011010 গ) 0111011 ঘ) 00101011
৪। (1110.0011)2 এর সমকক্ষ হেক্সাডেসিমাল সংখ্যা কোনটি?
ক) E.3 খ) E.8 গ) E.C ঘ) C.E
৫। 7B কে বাইনারিতে প্রকাশ করলে সংখ্যাটি হবে-
ক) 1011001 খ) 1111011 গ) 1101111 ঘ) 1001101
৬। (১১১০.১১)২ এর সমকক্ষ হেক্সাডেসিমেলের সংখ্যা কোনটি?
ক) E.A খ) E.C গ) C.E ঘ) E.3
৭। (11011.110111)2 এর সমতুল্য হেক্সাডেসিমাল সংখ্যা কত?
ক) 1B.37 খ) 1B.DC গ) D8.DC ঘ) D8.37
৮। (1010)2 এর সমতুল্য মান-
i. (10)10 ii. (12)8 iii. (14)16
নিচের কোনটি সঠিক?
ক) i ও ii খ) i ও iii গ) ii ও iii ঘ) i,ii ও iii
নিচের উদ্দীপক পড় এবং ৯ ও ১০ নং প্রশ্নের উত্তর দাওঃ
মি.আতিক কামালকে বলল, “তোমার বয়স কত?” কামাল বলল যে তার বয়স (101101)2 ।
৯। কামালের বয়সের সমকক্ষ অক্টাল সংখ্যা হলো-
ক) (25)8 খ) (35)8 গ) (55)8 ঘ) (65)8
১০। দশ বছর পর কামালের বয়স বাইনারিতে কত হবে?
ক) (101011)2 খ) (101110)2 গ) (101111)2 ঘ) (110111)2
১১। (১১০১১০)২ এর সমকক্ষ মান-
i. (৬৬)৮ ii. (৫৪)১০ iii. (৩৬)১৬
নিচের কোনটি সঠিক?
ক) i ও ii খ) i ও iii গ) ii ও iii ঘ) i,ii ও iii
তৃতীয় অধ্যায়ের সকল MCQ দেখতে ক্লিক করো
Written by,
- Mizanur Rahman (Mizan)
- Lecturer in ICT, Shaheed Bir Uttam Lt. Anwar Girls’ College , Dhaka Cantonment
- Founder & Author at www.edupointbd.com
- Software Engineer at mands IT
- Former Lecturer in ICT, Cambrian College, Dhaka
- Contact: 01724351470

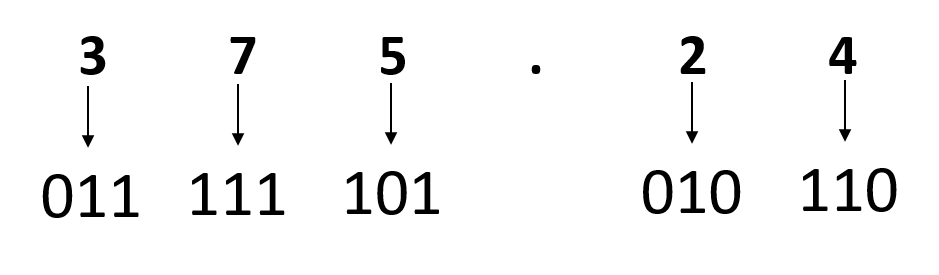
(375.24)8 সংখ্যাকে বাইনারি সংখ্যায় রূপান্তর। এটাকি একটু বোঝানো যাবে?
আমি বোঝতে পারতাছিনা।
(১০১০১০.০১০১)২ ডেসিমাল স;খায় রুপান্তর কর।
রুবিনার বয়স (3A)বাইনারি সংখ্যা কত হবে
0111010
Decimal to Bionary korte kon bit ba code use hobe
১০ নাম্বারের উত্তর কি হবে?