At the end of this lesson-
- You will be able to explain the concept of signed number.
- You will be able to explain the different methods of representing signed number in computer system.
- You will be able to do addition and subtraction of signed number using 2’s complement form.
- You will be able to explain basic concept of register.
Go for Bangla Version
In general, we represent the positive (unsigned) numbers without any sign indication and negative numbers with ‘minus’ (negative sign) sign before them. But these are not applicable for computing in the digital systems like, computers , as the data is represented in binary number system. So to represent the sign a special notation is required.
An extra bit is added before the actual value to represent the signed number in the binary method. This extra bit is called the signed bit. If the bit is 0, the number is positive and if the bit is 1, the number is assumed to be negative.
As we cannot feed positive or negative signs to the digital system, these should be represented in some other ways. There are three common ways to represent negative numbers within the computer. They are
- Signed magnitude form
- 1’s compliment form
- 2’s complement form
In this case, the representation of positive numbers is the same in all three forms. That is, in the case of a positive number, except signed bit all the bits represent the actual value of the number. However, in case of negative numbers, the presentation is different.
In order to represent numbers with the above mentioned three methods, one must have a basic idea about the register The register is a circuit consisting of a set of flip-flops and gates that serve as temporary memory. Each of these flip-flops can store one binary bit. A n bit register can hold binary data of n bit. That is, 8-bit register, 16-bit register, 32-bit register, etc. can hold 8, 16 & 32 bit data respectively.
In the case of a 8-bit register, the right most 7-bits are the data bits and the left most bit is the sign bit. Similarly, in the case of a 16-bit register, the right most 15-bits are the data bits and the left most bit is the sign bit. That is, in the case of a n-bit register, the right most n-1 bits are the data bits and the left most bit is the sign bit.
How many bits of the register to use depends on the given number. If a number of data bits is more than 7 bits then 16-bits register should be used and if the data bit is more than 15-bits then you should use 32-bits resisters.
Sign Magnitude form:
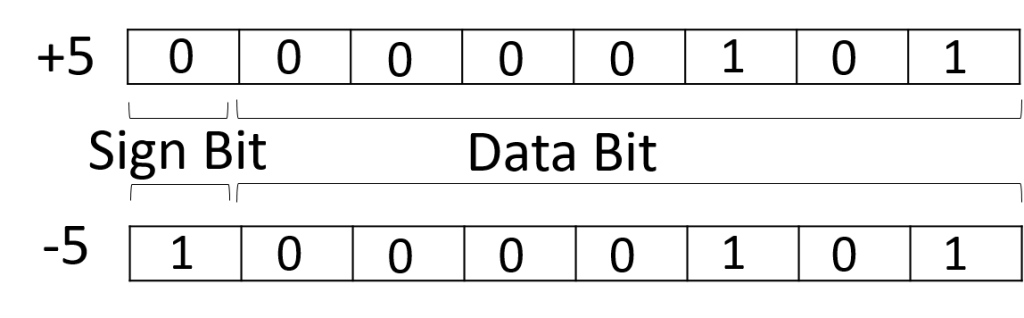
For n bit binary number, 1 bit is reserved for sign symbol. If the value of sign bit is 0, then the given number will be positive, else if the value of sign bit is 1, then the given number will be negative. Remaining (n-1) bits represent magnitude of the number. Since magnitude of number zero (0) is always 0, so there can be two representation of number zero (0), positive (+0) and negative (-0), which depends on value of sign bit.
Hence these representations are ambiguous generally because of two representation of number zero (0). Generally sign bit is a most significant bit (MSB) of representation. The range of Sign-Magnitude form is from (2(n-1)-1) to (2(n-1)-1).
Representation of +5 and -5 using sign magnitude form in 8-bit register:
In this case, if the data bit is less than 7-bit, then the rest will be filled with 0.
1’s complement form:
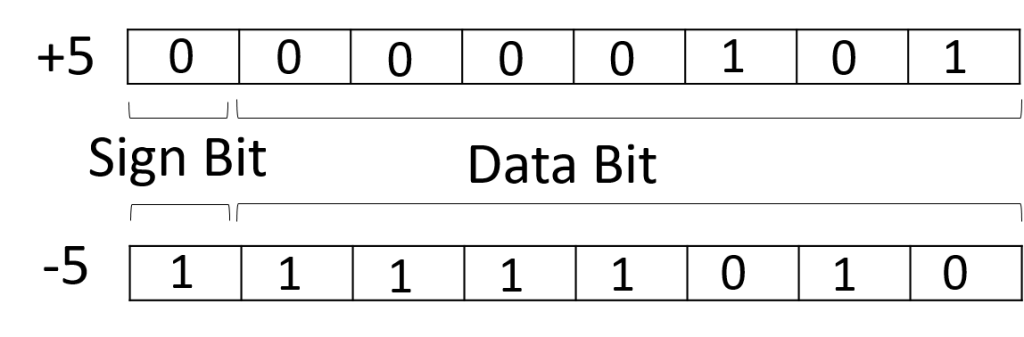
Since, 1’s complement of a number is obtained by inverting each bit of given number. So, we represent positive numbers in binary form and negative numbers in 1’s complement form. There is extra bit for sign representation. If value of sign bit is 0, then number is positive and you can directly represent it in simple binary form, but if value of sign bit 1, then number is negative and you have to take 1’s complement of given binary number. You can get negative number by 1’s complement of a positive number and positive number by using 1’s complement of a negative number. Therefore, in this representation, zero (0) can have two representation, that’s why 1’s complement form is also ambiguous form. The range of 1’s complement form is from (2(n-1)-1) to (2(n-1)-1).
Representation of +5 and -5 using 1’s complement form in 8-bit register:
In this case, if the data bit is less than 7-bit, then the rest will be filled with 0.
2’s complement form:
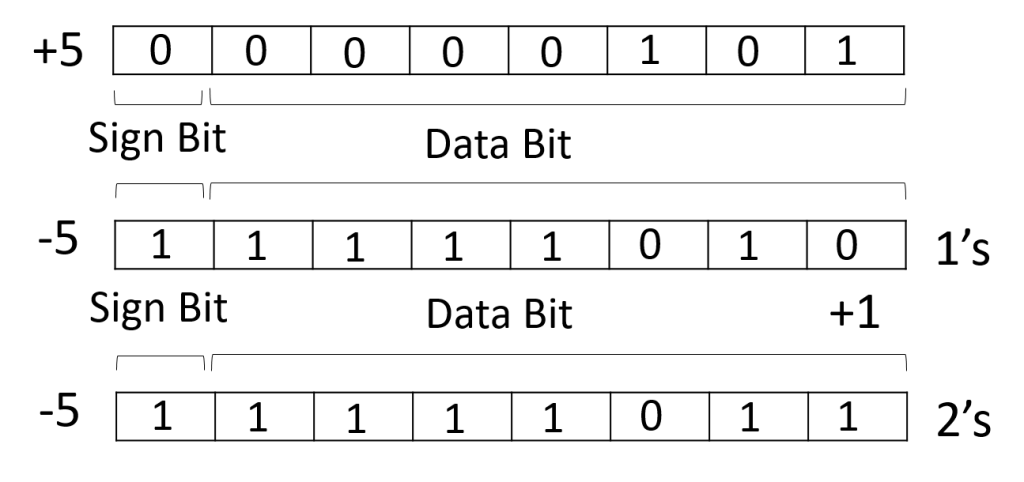
Since, 2’s complement of a number is obtained by inverting each bit of given number plus 1 to least significant bit (LSB) (one’s complement + 1). So, we represent positive numbers in binary form and negative numbers in 2’s complement form. There is extra bit for sign representation. If value of sign bit is 0, then number is positive and you can directly represent it in simple binary form, but if value of sign bit 1, then number is negative and you have to take 2’s complement of given binary number. You can get negative number by 2’s complement of a positive number and positive number by directly using simple binary representation. If value of most significant bit (MSB) is 1, then take 2’s complement from, else not. Therefore, in this representation, zero (0) has only one (unique) representation which is always positive. The range of 2’s complement form is from (2(n-1)) to (2(n-1)-1).
Representation of +5 and -5 using 2’s complement form in 8-bit register:
In this case, if the data bit is less than 7-bit, then the rest will be filled with 0.
Importance of 2’s Complement form:
- The subtraction process can be completed by using an additional processes.
- A simple logical circuit building becomes easier.
- By using this form, addition and subtraction process can be completed by the same logical circuit.
Addition in 2’s Complement Form:
1. The given signed numbers have to be represented in 2’s complement form.
2. Then add the binary of the obtained value.
3. If the extra carry bit is present in the sum (that is, if the sum is greater than 8 bits in the case of a 8-bit register, then, the left most bit is called a carry bit), it should be omitted.
4. The number thus obtained will be the sum of the given numbers.
Example-1: Add -25 and +12 in case of 8-bit register.

Example-2: Add +25 and -12 in case of 8-bit register.
Example-3: Add -25 and -12 in case of 8-bit register.
Example-4: Add +25 and +12 in case of 8-bit register.
Subtraction in 2’s Complement Form:
1. The number which will be subtracted should change the sign and then has to be represented in 2’s complement form.
2. The second signed number has to be represented in 2’s complement form.
3. Then add the obtained binary value (addition also be done in subtraction)
4. If the extra carry bit is present in the sum (that is, if the sum is greater than 8 bits in the case of a 8-bit register, then, the left most bit is called a carry bit), it should be omitted.
5. Thus the number obtained will be the difference of the given numbers.
Example-1: Subtract +12 from -25 in case of 8-bit register.
= – 25 – 12
= – 25 + (-12)

Example-2: Subtract -12 from +25 in case of 8-bit register.
Example-3: Subtract -12 from -25 in case of 8-bit register.
Example-4: Subtract +12 from +25 in case of 8-bit register.
Lesson Evaluation-
Knowledge Based Questions:
a. What is signed number?
a. What is sign bit?
a. What is 1’s complement?
a. What is 2’s complement?
Comprehension Based Questions:
b. What do you understand by signed number? Explain.
b. Why 2’s complement is important? -Explain.
b. Subtraction can be performed using addition.–Explain.
Creative Questions:
According to the stem answer the following questions:
The ICT teacher was teaching number system. He asked a student’s roll, he answered (375)10. The teacher commented that the last year’s roll number (17C)16 was good.
d) Determine the difference between roll numbers by addition.
d) Subtract the number of the stem using the operation indicated by ICT teacher.
d) Find out doing addition how many pencil is left after giving it to Pavel?
Multiple Choice Questions:
1. Which method is used in computer system?
a) 1’s Complement
b) 2’s Complement
c) 10’s Complement
d) 9’s Complement
2. Which one is the formula of 2’s Complement form?
a) 1’s complement + 1
b) 1’s complement – 1
c) 1’s complement + Binary value
d) 1’s complement + 10
3. What is the 2’s complement of (12)10?
a) 00001100 b) 11111100
c) 11110011 d) 11110100
Written by,
- Mizanur Rahman (Mizan)
- Lecturer in ICT, Shaheed Bir Uttam Lt. Anwar Girls’ College , Dhaka Cantonment
- Founder & Author at www.edupointbd.com
- Software Engineer at mands IT
- Former Lecturer in ICT, Cambrian College, Dhaka
- Contact: 01724351470