Boolean Algebra, Boolean Postulates and Boolean Theorems

At the end of this lesson-

You will be able to explain the characteristics of Boolean Algebra.
You will be able to explain Boolean variable, constant and complement.
You will be able to explain Boolean postulate and Duality Principle.
You will be able to explain different Boolean Theorems.

Go For Bangla Version

Boolean Algebra:

Boolean Algebra is an algebra, which deals with binary numbers & binary variables. Boolean Algebra is used to analyze and simplify the digital (logic) circuits. It is also called as Binary Algebra or logical Algebra or Switching algebra. A mathematician, named George Boole discovered a relation between mathematics and logic, based on this relation he developed a kind of algebra in 1854 called Boolean algebra.

Boolean algebra basically developed based on logic TRUE and logic FALSE. On the other hand all kind of digital devices work in binary method. This Boolean algebra is used in these digital devices to solve mathematical and logical problem.

It is possible to solve all the mathematical and logical problems in digital devices by converting logic TRUE and logic FALSE of Boolean algebra into 1 and 0 respectively.

Characteristics of Boolean Algebra:

In Boolean algebra, only two digits ‘0’ and ‘1’ are used.
As Boolean variables have two values, Boolean algebra is a much simpler method than decimal algebra.
Boolean algebra cannot use any fraction, logarithm, square, negative number, imaginary number etc.
In Boolean algebra, all mathematical operations are done only with logical addition, multiplication and complement. No geometric or trigonometric formula can be used in Boolean algebra.

The following elements are in Boolean algebra-

Basic symbols: Two basic symbol; TRUE/ON/1 and FALSE/OFF/0

Operators: Three Operators; AND ( . ), OR ( + ), NOT( ¯ )

Basic Operations in Boolean algebra:

AND Operation Or Logical Multiplication
OR Operation Or Logical Addition
NOT Operation Or Logical Inversion

Theorems: Different Boolean Theorems, De Morgan’s theorem, Duality Principle etc.

Boolean variables:

The variables used in Boolean algebra are called as Boolean variables. Whose Values are changed and can be either 0 or 1. For example, C = A + B, here A and B are the Boolean variables.

Boolean constant:

In Boolean algebra whose values will remain unchanged is called Boolean Constant. For example, Y = A + 0 + 1, Here, 0 and 1 are Boolean constant.

Boolean complement:

The value of any variable in Boolean algebra is 0 or 1. These 0 and 1 are called Boolean complements of each other. Boolean complement is expressed with an ” ¯ ” symbol. In the language of mathematics, A´ is the complement of A.

Boolean Postulates:

The rules followed by OR Operation ( Logical addition), AND Operation (Logical Multiplication) and NOT Operation ( Logical Inversion) in Boolean Algebra is called Boolean Postulates. Boolean Postulates are three types. They are-

Boolean Postulates of OR
Boolean Postulates of AND
Boolean Postulates of NOT

Boolean Postulates of OR:

The rules followed by OR Operation ( Logical addition) in Boolean Algebra is called Boolean Postulates of OR. The rule is – If any value among values is 1, result will be 1, Otherwise result will be 0.

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 1

Boolean Postulates of AND:

The rules followed by AND Operation (Logical Multiplication) in Boolean Algebra is called Boolean Postulates of AND. The rule is – If any value among values is 0, result will be 0, Otherwise result will be 1.

0 . 0 = 0

0 . 1 = 0

1 . 0 = 0

1 . 1 = 1

Boolean Postulates of NOT:

The rules followed by NOT Operation ( Logical Inversion) in Boolean Algebra is called Boolean Postulates of NOT. Complement of 1 is 0 and Complement of 0 is 1.

1´ = 0

0´ = 1

Note− The complement of complement of any Boolean variable is equal to the variable itself. i.e., $x^{'}$ ’=x.

Duality Principle:

This theorem states that the dual of the Boolean function is obtained by interchanging the logical AND operator with logical OR operator and zeros with ones. For every Boolean function, there will be a corresponding Dual function.

Let us make the Boolean equations $r e l a t i o n s$ that we discussed in the section of Boolean postulates and basic laws into two groups. The following table shows these two groups.

Group1	Group2
x + 0 = x	x.1 = x
x + 1 = 1	x.0 = 0
x + x = x	x.x = x
x + x’ = 1	x.x’ = 0
x + y = y + x	x.y = y.x
x + $y + z$ = $x + y$ + z	x. $y . z$ = $x . y$ .z
x. $y + z$ = x.y + x.z	x + $y . z$ = $x + y$ . $x + z$

In each row, there are two Boolean equations and they are dual to each other. We can verify all these Boolean equations of Group1 and Group2 by using duality theorem.

Boolean Theorems:

Basic Theorems:

Annulment law – a variable ANDed with 0 gives 0, while a variable ORed with 1 gives 1, i.e.,

A.0 = 0
A + 1 = 1

Identity law – in this law variable remain unchanged it is ORed with ‘0’ or ANDed with ‘1’, i.e.,

A.1 = A
A + 0 = A

Idempotent law – a variable remain unchanged when it is ORed or ANDed with itself, i.e.,

A + A = A
A.A = A

Complement law – in this Law if a complement is added to a variable it gives one, if a variable is multiplied with its complement it results in ‘0’, i.e.,

A + A’ = 1
A.A’ = 0

Double negation law – a variable with two negation its symbol gets cancelled out and original variable is obtained, i.e.,

((A)’)’=A

Commutative law – a variable order does not matter in this law, i.e.,

A + B = B + A
A.B = B.A

Associative law – the order of operation does not matter if the priority of variables are same like ‘*’ and ‘/’, i.e.,

A+(B+C) = (A+B)+C
A.(B.C) = (A.B).C

Distributive law – this law governs opening up of brackets, i.e.,

A.(B+C) = (A.B)+(A.C)
A+(B.C) = (A+B).(A+C)

Absorption or Secondary law –:-This law involved absorbing the similar variables, i.e.,

A.(A+B) = A

A + AB = A

A’ + AB = A’+B

A+A’B = A+B

Switching Circuits for Boolean Theorems:

Boolean Theorem	Equivalent Switching Circuit
A + 1 = 1
A . 0 = 0
A + 0 = A
A . 1 = A
A + A = A
A . A = A
A + A = 1
A . A = 0
A+B = B+A
A.B = B.A

Proof of Some Basic Boolean Theorems:

In case of Boolean Addition:

Lesson Evaluation-

Knowledge Based Questions:

a. What is Boolean algebra?

a. What is Boolean variable?

a. What is Boolean constant?

a. What is Boolean complement?

a. What is a Boolean postulate?

a. What is Boolean duality principle?

Go For Answer

Comprehension Based Questions:

b. “1+1+1=1” –Explain.

b. “T+T=T” – Explain.

b. “A+1+1 =1”- Explain.

b. In which argument 1+1=1 and 1+1=10 can be written? –Explain.

b. ‘Binary 1+1 and Boolean 1+1 are not same’ –Explain.

b. “Binary addition and Boolean addition are not same”-Explain.

Go For Answer

Creative Questions:

Multiple Choice Questions:

1. Who is the inventor of Boolean algebra?

a) George Bool b) Newton c) Pascal d) Bill Gates

2. In which year did George Bool find the relation between mathematics and logic?

a) 1945 b) 1833 c) 1944 d) 1854

3. Boolean algebra is based on which of the following relationships?

a) Logic and Gate b) Algebra and Arithmetic c) Mathematics and Logic d) Mathematics and Wisdom

4. If A = 0 and B = 1, then AB=?

a) 0 b) 1 c) 2 d) 3

5. When logical multiplication of A, B & C will be 1?

a) Three values are 1 b) Three values are 0 c) Any value is 1 d) Any two values are 1

6. Result for Logical addition of A, B & C will be 1, if

i. Any value is 1 ii. Any two values are 1 iii. Three values are 0

Which one is correct?

a) i & ii b) i & iii c) ii & iii d) i, ii & iii

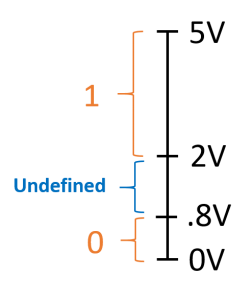
7. In digital system which voltage level is not defined?

a) +0 V – +0.8 V b) +0.8 V – +2 V c) +2 V – +5V d) +0.8 V – +5 V

Written by,

Mizanur Rahman (Mizan)
Lecturer in ICT, Shaheed Bir Uttam Lt. Anwar Girls’ College , Dhaka Cantonment
Founder & Author at www.edupointbd.com
Software Engineer at mands IT
Former Lecturer in ICT, Cambrian College, Dhaka
Contact: 01724351470

Spread the love