At the end of this lesson-
- You will be able to explain De Morgan’s Theorem.
- You will be able to create truth table.
- You will be able to create Boolean function from a truth table.
- You will be able to prove De Morgan’s theorem using truth table.
- You will be able to prove any Boolean equation using truth table.
Go for Bangla Version
De Morgan’s Theorem
Mathematician De Morgan discovered two theorems for Boolean function simplification.
First Theorem: It states that the complement of logical OR of at least two Boolean variables is equal to the logical AND of each complemented variable. De Morgan’s theorem with n Boolean variables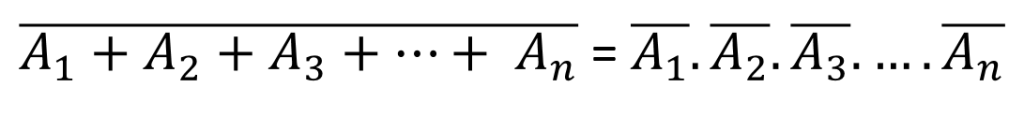
De Morgan’s theorem with 2 Boolean variables A and B can be represented as
(A+B)’ = A’.B’
De Morgan’s theorem with 3 Boolean variables A, B & C can be represented as
(A+B+C)’ = A’.B’.C’
Second Theorem: It states that the complement of logical AND of n Boolean variables is equal to the logical OR of each complemented variable.
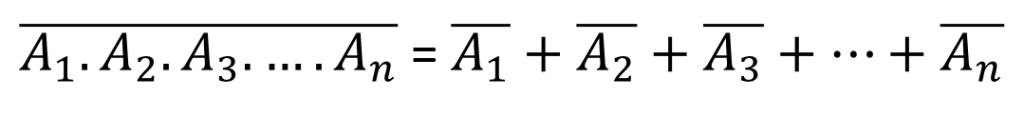
De Morgan’s theorem with 2 Boolean variables A and B can be represented as
(A.B)’ = A’ + B’
De Morgan’s theorem with 3 Boolean variables A, B & C can be represented as
(A.B.C)’ = A’ + B’ + C’
Truth Table:
In a standard Boolean Expression, the input and output information of any Logic Gate or circuit can be plotted into a standard table to give a visual representation of the switching function of the system.
The table that used to represent the Boolean expression of a logic gate function is commonly called a Truth Table. Truth table of a logic gate shows each possible input combination to the gate or circuit with the resultant output depending upon the combination of these input(s).
If a Boolean function has n number of variables, There are 2n possible input combinations and 2n outputs in the truth table.
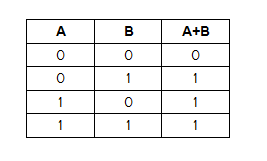
Lets see the truth table for Boolean expression F= A+B
As input variables A & B, There are 22 possible input combinations and 2n outputs-
Converting Truth Tables into Boolean Expressions:
There are two ways to convert truth tables into Boolean Expression-
- Using Min-term/ SOP
- Using Max-term/ POS
Using Min-term or product-terms/ SOP:
A min-term is a product (AND) of all variables in the truth table in direct or complemented form. A min-term has the property that it is equal to 1.
Sum-Of-Products, or SOP, Boolean expressions may be generated from truth tables quite easily, by determining which rows of the table have an output of 1, writing one min-term/ product-term for each row, and finally summing all the min-term/ product-terms. This creates a Boolean expression representing the truth table as a whole.
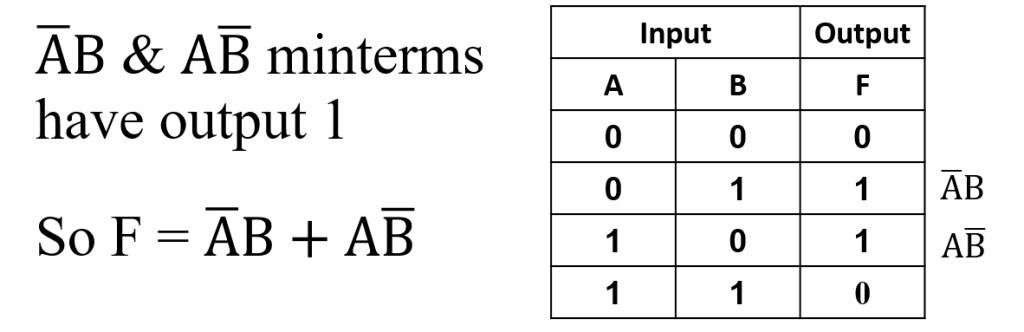
Finally, we join these two Boolean product expressions together by addition, to create a single Boolean expression describing the truth table as a whole.
Sum-Of-Products expressions lend themselves well to implementation as a set of AND gates (products) feeding into a single OR gate (sum).
Using Max-term or sum-term/ POS:
A max-term is a sum (OR) of all variables in the truth table in direct or complemented form. A max-term has the property that it is equal to 0.
Product-Of-Sums, or POS, Boolean expressions may also be generated from truth tables quite easily, by determining which rows of the table have an output of 0, writing one max-term/ sum-term for each row, and finally multiplying all the max-term /sum-terms. This creates a Boolean expression representing the truth table as a whole.

Product-Of-Sums expressions lend themselves well to implementation as a set of OR gates (sums) feeding into a single AND gate (product).
Proving Boolean Expression using truth table:
Compare all product terms of the two expressions. If they are identical, the two expressions are equal.
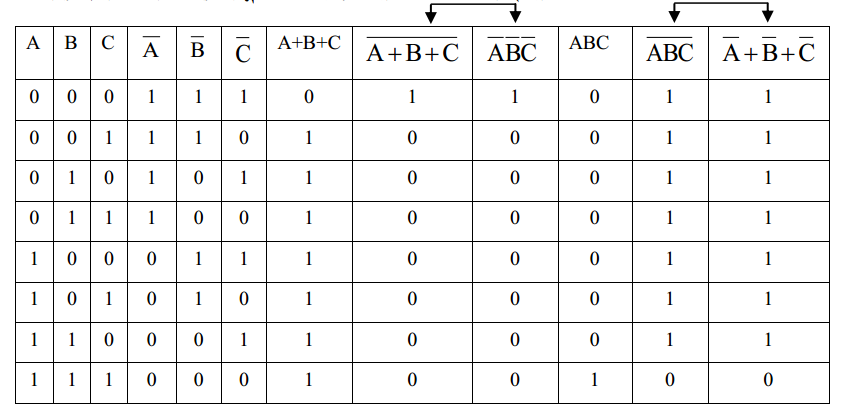
Proof of the following two De Morgan’s Theorems for two variables using Truth table:
- (A+B)’ = A’.B’
- (A.B)’ = A’ + B’
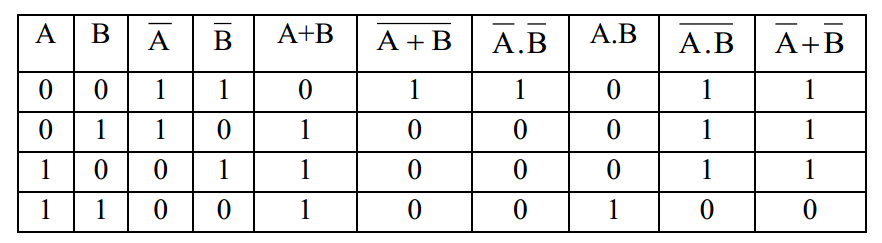
Proof of the following two De Morgan’s Theorems for three variables using Truth table:
- (A+B+C)’ = A’.B’.C’
- (A.B.C)’ = A’ + B’ + C’
Lesson Evaluation-
Knowledge Based Questions:
a. What is truth table?
a. Write down the De-Morgan’s Theorems.
Comprehension Based Questions:
b. Describe De-Morgan’s theorem for n number of variables.
b. Prove De-Morgan’s theorem.
b. Why truth table is used?
b. Write difference between min-term and max-term.
Creative Questions:
According to the following stem answer the questions:
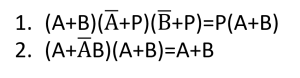
c) Prove equation-2 using truth table.
d) How many input combinations are needed for equation-1 to prove? Analyze with truth table.
According to the following stem answer the questions:
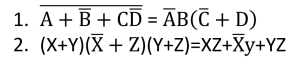
c) Prove equation-2 using truth table.
d) How many input combinations are needed for equation-1 to prove? Analyze with truth table.
Multiple Choice Questions:
1. Which one is the function of truth table?
a) Value determination
b) Justify the truthiness
c) Input determination
d) Output determination
Written by,
- Mizanur Rahman (Mizan)
- Lecturer in ICT, Shaheed Bir Uttam Lt. Anwar Girls’ College , Dhaka Cantonment
- Founder & Author at www.edupointbd.com
- Software Engineer at mands IT
- Former Lecturer in ICT, Cambrian College, Dhaka
- Contact: 01724351470