Third Chapter

HSC ICT Chapter 3 MCQ Board Question Solution Number System

December 15, 2023December 15, 2023Mizanur Rahman

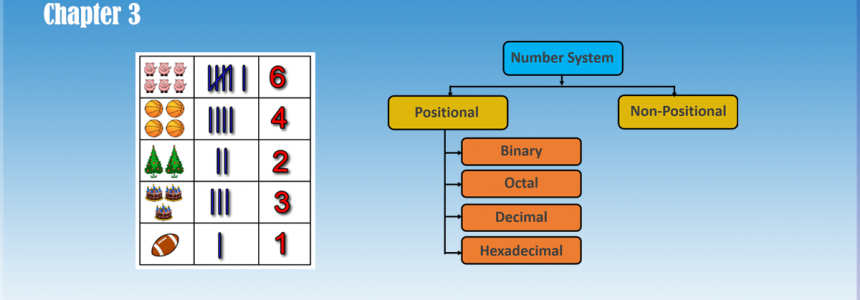
HSC ICT Chapter 3 Board Questions with Important MCQ Solutions. I hope that solving these questions will give you a good preparation. Number system can be mainly divided into how many types? [Ctg. Board 2016] a) 2 b) 3 c) 8 d) 10 How many types of number system depends on the base? [Jas. Board 2017] a) 2 b) 4 c) 8 d) 10 How many bits are there in the number 1011? [Ma. Board 2019] a) 2 b) 4 c) 8 d) 10 In (1110)₂ number '0' indicates- a) BOS b) BCD c) LSB d) MSB What is the sma...

HSC ICT Chapter 3 : Comprehension Based Questions & Answers

April 11, 2020September 11, 2023Mizanur Rahman

How to write answers to a comprehension based question? ⇒ 'Comprehension' refers to the ability to understand the meaning of a topic. It can be the ability to understand any information, policy, formula, rule, procedure, process etc. ⇒ Perceptual level is the second level of thinking skills. This question is given in 'b'. Such questions do not directly ask for textbook-like details. So the student has to explain or describe the content in his own way. ⇒ Marks of comprehension based question will be 2. Out of which 1 is for knowledge and 1 is for comprehension. ⇒ Comprehension based q...

HSC ICT Chapter 3 : Knowledge Based Questions & Answers

April 10, 2020June 9, 2023Mizanur Rahman

How to write answers to knowledgebase questions? The knowledgebase question is given to test the memory. That is, you can answer this part by memorizing any information from the text book. Answers should be given in one sentence or a maximum of three sentences as per the demand of the question. Mark allotted to this question is 1. Number System: What is number? What is digit? [Madrasa Board-2017] What is the number system? [Jessore Board-2017, Madrasa Board-2016] What is non-positional number system? What is positional number system? What is binary number system...

Adder, Half Adder, Full Adder, Full Adder implementation using Half Adder

March 23, 2020September 10, 2022Mizanur Rahman

At the end of this lesson- 1. You will be able to explain Adder circuit. 2. You will be able to describe Half Adder circuit. 3. You will be able to describe Full Adder circuit. 4. You will be able to implement Full adder circuit using Half adder circuit. 5. You will be able to explain binary adder circuit. Go for Bangla Version An adder is a combinational circuit or digital circuit in electronics that implements or performs addition of numbers. It is mainly designed for the addition of binary number, but they can be used in various other applications like b...

Encoder and Decoder | Difference Between Encoder and Decoder

March 22, 2020August 7, 2023Mizanur Rahman

At the end of this lesson- 1. You will be able to explain encoder. 2. You will be able to describe the uses of encoder. 3. You will be able to explain decoder. 4. You will be able to describe the uses of decoder. 5. You will be able to differentiate encoder and decoder. Go for Bangla Version What is Encoder? An Encoder is a combinational circuit that produces a binary code equivalent to the input, which is active High. In other words, Encoder is a circuit which converts the analog signal into the digital signal. Encoders are digital circuit used for encodin...

Logic Circuit for Logic function & Logic function from Logic circuit

March 22, 2020September 10, 2022Mizanur Rahman

At the end of this lesson- 1. You will be able to implement any function. 2. You will be able to determine function from any circuit. Go for Bangla Version Implementation of any function: The function may need to be implemented with only basic gates. The function may need to be implemented with only universal gates. The function may need to be implemented using any type of gates. After simplifying the function, It may need to be implemented by basic or universal gates. The following rules or sequences are followed to implement the function...

NAND & NOR gates as Universal Gates

March 22, 2020September 10, 2022Mizanur Rahman

At the end of this lesson- You will be able to prove the universality of NAND and NOR gates. You will be able to implement AND, OR & NOT gate using only NAND gate. You will be able to implement AND, OR & NOT gate using only NOR gate. You will be able to implement XOR & XNOR gate using only NAND gate. You will be able to implement XOR & XNOR gate using only NOR gate. Go for Bangla Version NAND gate as Universal Gate: Implementation of NOT gate using only NAND gate Implementation of AND gate using only NAND gate: ...

Universal Gates (NAND, NOR) & Special Gates (XOR, XNOR)

March 22, 2020September 10, 2022Mizanur Rahman

At the end of this lesson- You will be able to explain compound gate. You will be able to describe the Universal gates. You will be able to describe NAND & NOR gates in details. You will be able to describe the Exclusive gates in details. You will be able to describe X-OR & X-NOR gates in details. Go for Bangla Version Compound/Composite Gates: A gate that is created using two or more basic gates is called a composite or compound gate. For example- AND Gate +NOT Gate = NAND Gate, OR Gate + NOT Gate = NOR Gate. Composite gates are two types. T...

Logic Gates & Basic Logic Gates (AND, OR & NOT)

March 21, 2020September 10, 2022Mizanur Rahman

At the end of this lesson- You will be able to explain logic gate. You will be able to describe the types of logic gate. You will be able to describe the basic gates in details. Go For Bangla Version Logic gates: A logic gate is a basic building block of a digital circuit, which is used to implement a Boolean function. It is an electronic circuit which makes logical decisions based on the combination of digital signals present on its inputs. It is an electronic circuit having one or more than one inputs and only one output. Types of Logic gates: Basic G...

Simplification of Boolean Expressions

March 21, 2020September 10, 2022Mizanur Rahman

At the end of this lesson- You will be able to describe the rules of simplifying the Boolean expressions. You will be able to simplify the Boolean expressions. You will be able to explain the importance of simplifying the Boolean expressions. Go for Bangla Version The Boolean functions are implemented through the Logic Gates. In this case the number of logic operators in the function is less then the number of logic gates in the implementation is less. This makes implementation easier and saves money. Therefore, the Boolean functions are simpli...

De Morgan’s Theorem and Truth table

March 21, 2020September 10, 2022Mizanur Rahman

At the end of this lesson- You will be able to explain De Morgan's Theorem. You will be able to create truth table. You will be able to create Boolean function from a truth table. You will be able to prove De Morgan's theorem using truth table. You will be able to prove any Boolean equation using truth table. Go for Bangla Version De Morgan’s Theorem Mathematician De Morgan discovered two theorems for Boolean function simplification. First Theorem: It states that the complement of logical OR of at least two Boolean variables is equal to the logical AN...

Boolean Algebra, Boolean Postulates and Boolean Theorems

March 21, 2020September 10, 2022Mizanur Rahman

At the end of this lesson- You will be able to explain the characteristics of Boolean Algebra. You will be able to explain Boolean variable, constant and complement. You will be able to explain Boolean postulate and Duality Principle. You will be able to explain different Boolean Theorems. Go For Bangla Version Boolean Algebra: Boolean Algebra is an algebra, which deals with binary numbers & binary variables. Boolean Algebra is used to analyze and simplify the digital (logic) circuits. It is also called as Binary Algebra or logical Algebra or Switching...

Code | BCD | EBCDIC | ASCII | Unicode

March 20, 2020September 10, 2022Mizanur Rahman

At the end of this lesson- You will be able to explain the concept of code. You will be able to explain BCD code. You will be able to explain alphanumeric code (EBCDIC, ASCII, Unicode). Go for Bangla Version In the computer system, digits, numbers, letters or special symbols are represented by a specific group of binary bits. This group is also called as binary code. The binary code is represented by the number as well as alphanumeric letter. Advantages of Binary Code Following is the list of advantages that binary code offers. Binary codes ar...

Signed Number | 1’s Compliment Form | 2’s Complement Form

March 17, 2020September 10, 2022Mizanur Rahman

At the end of this lesson- You will be able to explain the concept of signed number. You will be able to explain the different methods of representing signed number in computer system. You will be able to do addition and subtraction of signed number using 2's complement form. You will be able to explain basic concept of register. Go for Bangla Version In general, we represent the positive (unsigned) numbers without any sign indication and negative numbers with ‘minus’ (negative sign) sign before them. But these are not applicable for computing in the digi...

Binary Addition | Octal Addition | Hexadecimal Addition

February 15, 2020September 17, 2022Mizanur Rahman

At the end of this lesson- 1. You will be able to do addition in different number systems. 2. You will be able to do Subtraction in different number systems. Go for Bangla Version Addition of different number system: Addition of decimal numbers: 1. If summation of decimal digits is equal or more than the base of decimal number system, subtract 10(base) from summation( continue subtraction until summation comes to less than 10 ) 2. Carry is how many times subtraction is occurred Example: Addition of (5689)10 and (7989)10 Addition of octal numbers: ...

Binary to Octal | Binary to Hexadecimal | Octal to Binary | Hexadecimal to Binary

February 15, 2020September 17, 2022Mizanur Rahman

At the end of this lesson- 1. You will be able to convert Octal & Hexadecimal to Binary Number system. 2. You will be able to convert Binary to Octal & Hexadecimal Number system. 3. You will be able to convert Octal to Hexadecimal Number system. 4. You will be able to convert Hexadecimal to Octal Number system. Go For Bangla Version Conversion among Non-Decimal that means Binary, Octal & Hexadecimal Number Systems: Step-01: Convert the number from any base to base 10. Step-02: Convert the number from base 10 to any base. That is, in case of non-decimal n...

Binary to Decimal | Octal to Decimal | Hexadecimal to Decimal

February 15, 2020September 17, 2022Mizanur Rahman

At the end of this lesson- 1. You will be able to convert a binary number into decimal number. 2. You will be able to convert a octal number into decimal number. 3. You will be able to convert a hexadecimal number into decimal number. Go For Bangla Version Other Base to Decimal Number System Same Rules for Both Integer and Fractional Number- Step-1: Multiply each digit of the given number by their positional value. Positional value of a digit = (base of given number)position of the digit [ In integer number, position of the digit starts from 0 (right to left) and in ...

Decimal to Binary | Decimal to Octal | Decimal to Hexadecimal

February 14, 2020September 17, 2022Mizanur Rahman

At the end of this lesson- 1. You will be able to convert a decimal number into binary number. 2. You will be able to convert a decimal number into octal number. 3. You will be able to convert a decimal number into hexadecimal number. Go for Bangla Version Number System Conversions: There are twelve sorts of conversions among four number systems. They are- The same rules can be divided into the following ways- Decimal Number System to Other Base Decimal Number System to Binary Number System Decimal Number System to Octal Number System Decimal Number Sys...

Number System | Binary, Octal, Decimal & Hexadecimal Number

February 14, 2020September 17, 2022Mizanur Rahman

At the end of this lesson- 1. You will be able to describe the history of number. 2. You will be able to differentiate number and digit. 3. You will be able to describe the types of number system. 4. You will be able to differentiate different types of number systems. Go For Bangla Version What is Number ? A number is a string of one or more digits which is used to count, quantify and measure something. For example, there are 20 students in a class ; Here 20 is a number. What is Digit ? A digit is a single numerical symbol of a number or the smalle...